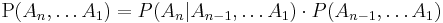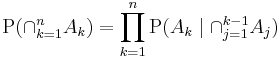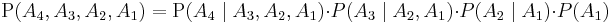Chain rule (probability)

In probability theory, the chain rule permits the calculation of any member of the joint distribution of a set of random variables using only conditional probabilities.

Consider an indexed set of sets $A_1, \ldots A_n$ . To find the value of this member of the joint distribution, we can apply the definition of conditional probability to obtain:

$\mathrm P(A_n, \ldots A_1) = P(A_n | A_{n-1}, \ldots A_1) \cdot P( A_{n-1}, \ldots A_1)$

Repeating this process with each final term creates the product

$\mathrm P(\cap_{k=1}^n A_k ) = \prod_{k=1}^n \mathrm P( A_k \mid \cap_{j=1}^{k-1} A_j )$

For example:

$\mathrm P(A_4, A_3, A_2, A_1) = \mathrm P(A_4 \mid A_3, A_2, A_1) \mathrm\cdot P(A_3 \mid A_2, A_1) \mathrm\cdot P(A_2 \mid A_1) \mathrm\cdot P(A_1)$

The rule is useful in the study of Bayesian networks, which describe a probability distribution in terms of conditional probabilities.

This rule is illustrated in the following example. Urn 1 has 1 black ball and 2 white balls and Urn 2 has 1 black ball and 3 white balls. Suppose we pick an urn at random and then select a ball from that urn. Let event A be choosing the first urn: P(A) = P(~A) = 1/2. Let event B be the chance we choose a white ball. The chance of choosing a white ball, given that we've chose the first urn, is P(B|A) = 2/3. The chance of choosing a white ball, given that we've chosen the second urn is P(B|~A) = 3/4. Event A, B would be their intersection; choosing the first urn and a white ball from it. The probability can be found by the chain rule for probability:

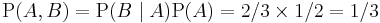$\mathrm P(A, B)=\mathrm P(B \mid A) \mathrm P(A) = 2/3 \times 1/2 = 1/3$ .

References

Russell, Stuart J.; Norvig, Peter (2003), Artificial Intelligence: A Modern Approach (2nd ed.), Upper Saddle River, New Jersey: Prentice Hall, ISBN 0-13-790395-2, http://aima.cs.berkeley.edu/ , p. 496.